国家开放大学离散数学（本）大作业第一部分+第二部分

 

下载以后，上传文件到对应任务即可

下方为题目演示，上方支付后即可获取答案下载链接

离散数学大作业

大作业时间为第1周到第17周，满分100分，由两部分组成。

提交作业方式有以下三种，请务必与辅导教师沟通后选择：

1. 将此次作业用A4纸打印出来，手工书写答题，字迹工整，解答题要有解答过程，完成作业后交给辅导教师批阅。

注意选择此种提交方式时仍然需要在网络课提交作业入口处上传说明文档，文档内注明“作业已由线下提交给辅导老师”。
2. 在线提交word文档．
3. 自备答题纸张，将答题过程手工书写，并拍照上传．

第一部分

一、公式翻译题（每小题2分，共10分）
1.将语句“我会英语，并且会德语．”翻译成命题公式．
2.将语句“如果今天是周三，则昨天是周二．”翻译成命题公式．
3.将语句“小王是个学生，小李是个职员．”翻译成命题公式．
4.将语句“如果明天下雨，我们就去图书馆.”翻译成命题公式．
5.将语句“当大家都进入教室后，讨论会开始进行．”翻译成命题公式．

二、计算题（每小题10分，共50分）
1．设集合A={1， 2， 3}，B={2， 3， 4}，C={2， {3}}，试计算
（1）AC； （2）A∩B； （3）(A∩B)×C．

2. 设G=<V，E>，V={v1， v2， v3， v4， v5}，E={(v1，v3) ， (v1，v5) ， (v2，v3) ， (v3，v4) ， (v4，v5) }，试

3．试画一棵带权为1， 2， 3， 3， 4的最优二叉树，并计算该最优二叉树的权．

4．求出如下所示赋权图中的最小生成树（要求写出求解步骤），并求此最小生成树的权．

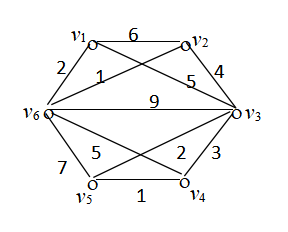
5. 求P→(Q∧R) 的析取范式与合取范式.

第二部分

从下列选题中选择一个感兴趣的主题，自主查阅文献资料进行深入的研究和学习，并形成一份至少一千字的总结报告。（40分）
答案：

离散数学在各学科领域的应用；